
“动力理论肯定了热和光是运动的两种方式,现在,它的美丽而晴朗的天空却被两朵乌云笼罩了,第一朵乌云出现在光的波动理论上;第二朵乌云出现在关于能量均分的麦克斯韦-玻尔兹曼理论上。”
——威廉.汤姆孙(开尔文男爵)
到19世纪末,许多科学家认为科学研究已经到了尽头,只剩下几个小问题,接下来只需要改进实验方法,将测量结果再提高精度就行。这种态度在某种程度上是有道理的,因为那时的科学已经取得了巨大的进步。
化学家们最终解决了一个看似无法克服的问题——即给元素分配一组自洽的原子质量。门捷列夫的伟大工作已经产生了元素周期表,尽管这种周期性行为在自然界中发生的根本原因尚不清楚。
在相关的物理学领域,牛顿力学被应用于行星运动,也可以解释其他复杂的自然现象。朗福德和焦耳证明了热和功的等价性,麦克斯韦的方程组将光学在电与磁的范围内统一起来。
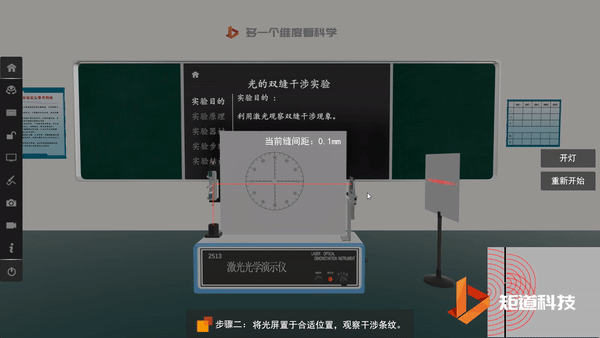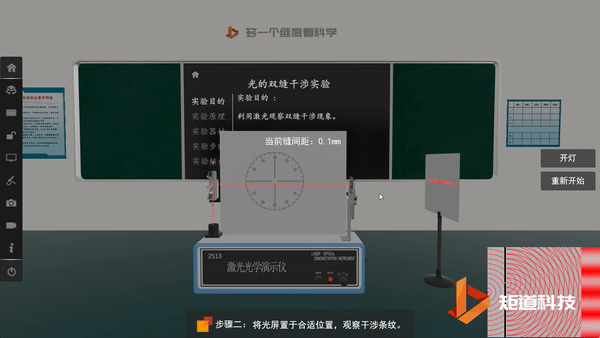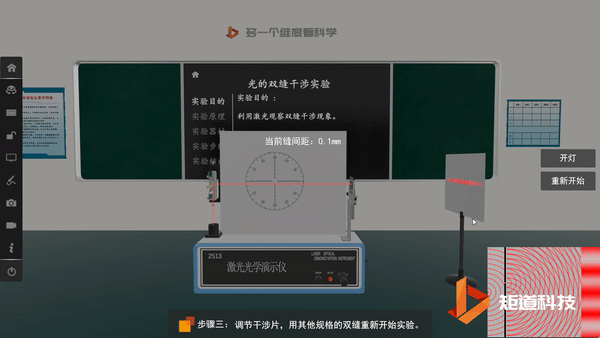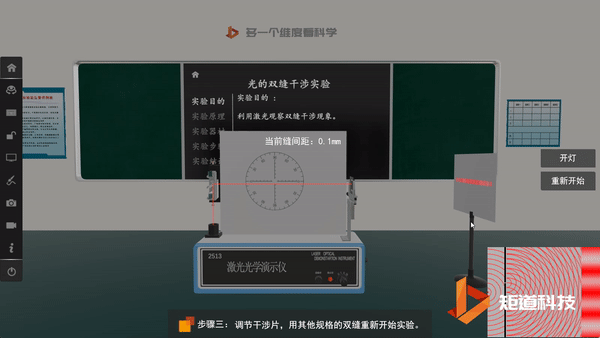
光的双缝干涉实验验证了光的波动性
进入20世纪,对于“两朵乌云”的研究导致了相对论和量子力学的诞生。其中量子力学是所有化学的基础,我们目前对原子结构和分子键的理解是基于量子力学的基本原理。
01
黑体辐射和光电效应
为了解释黑体辐射,德国物理学家普朗克做出假定:组成黑体的震动着的带电微粒的能量只能是某一最小能量值ε的整数倍。他把这个不可再分的最小能量值ε叫做能量子。
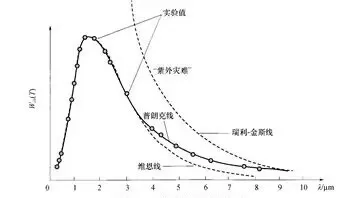
黑体辐射的光谱分布曲线
后来,为了解释光电效应,爱因斯坦将普朗克的观点更进一步,假定电磁波本身的能量也是不连续的,即认为光本身就是由一个个不可分割的能量子组成,频率为v的光的能量子为hv。其中h为普朗克常量,这些能量子后来被称为光子。
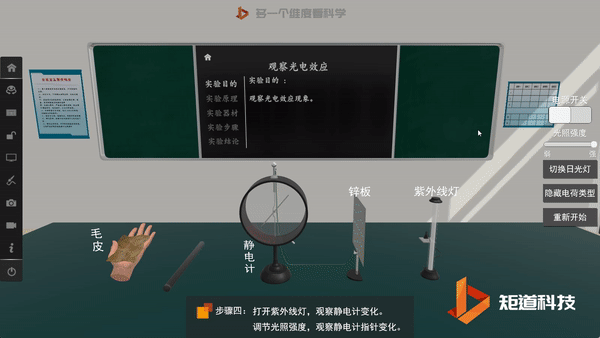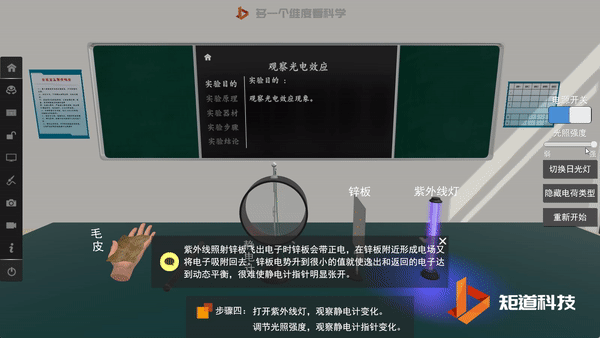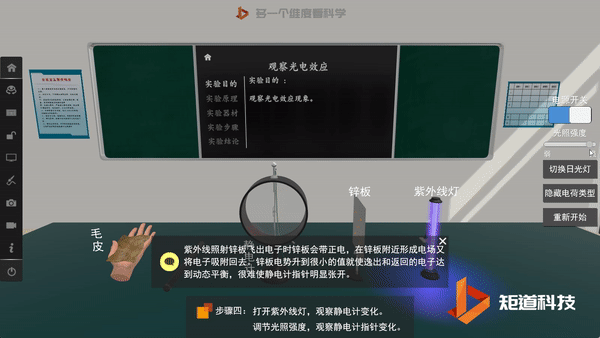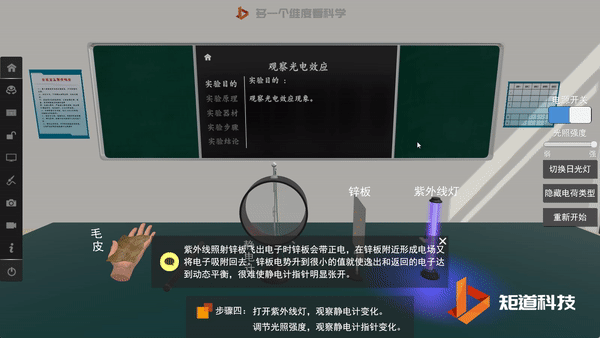
光电效应
美国物理学家康普顿更进一步,在解释后世被称为康普顿效应的现象时,他认为光子不但具有能量,而且具有动量,光子的动量p与光的波长λ和普朗克常量h有关。关系式为

此后,人们意识到,光既有波动性,也有粒子性,或者说,光具有波粒二象性。
02
德布罗意波
1924年,法国物理学家德布罗意将波粒二象性推广到实物粒子,如电子、质子等。他提出假设:每一个运动的粒子都有一个对应的波相凉席。粒子的动量p跟它对应的波的波长λ之间,遵从如下关系:
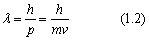
虽然关于实物粒子具有波动性的假说看上去难以理解,但仅仅过了3年,戴维森和G.P.汤姆孙分别用单晶和多晶做了电子束衍射的实验,得到了相应的衍射图样,证实了电子的波动性。

G.P.汤姆孙,他的父亲J.J.汤姆孙因发现电子而闻名
03
玻尔的原子模型
在传统的卢瑟福核式原子模型中,氢原子可以被描绘成一个中心的、相当大的原子核,带有一个关联的电子。由于原子核带正电,电子带负电,根据库仑定律,两者之间将存在一个束缚力:
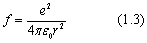
其中e是电子和质子的带电量,r是原子半径,ε0是真空中的介电常数。
因为原子核的质量比电子大得多,我们可以认为原子核是固定的,而电子是围绕它旋转的,因此力的大小也可以根据圆周运动的向心力公式得出:
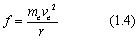
由于库仑力提供向心力,可以得出
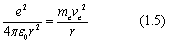
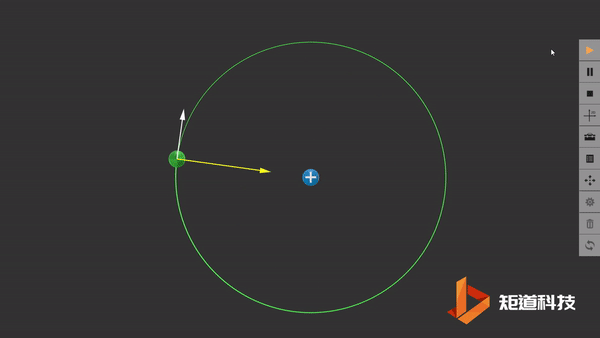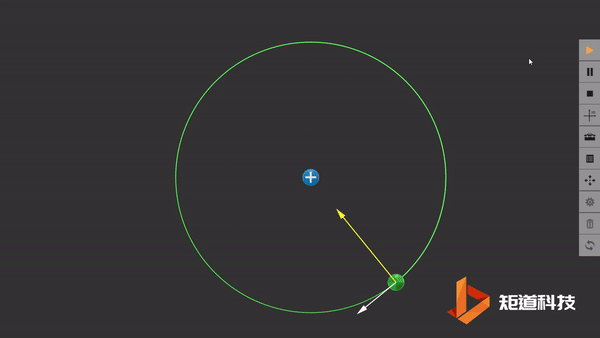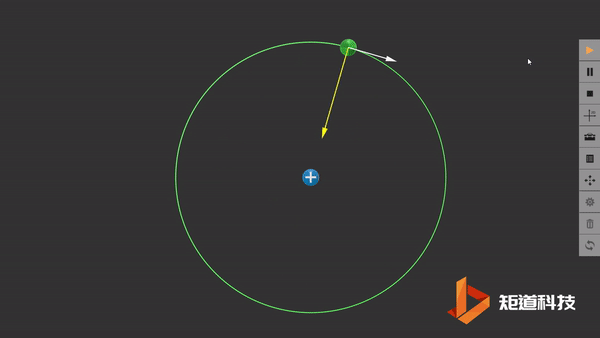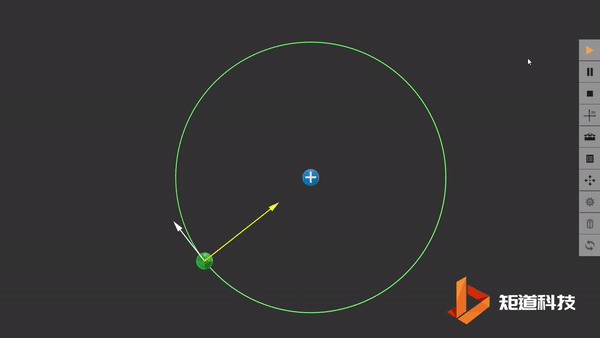
传统原子行星模型中的假想轨道
我们在这里默认电子以半径为r的圆形轨道围绕固定的原子核旋转。然而,在经典物理中,这种速度不断改变的运动电荷应该发射电磁辐射并损失能量,最终电子会坠入原子核中。因此原子在卢瑟福模型中应该是一个不稳定的模型,这与事实不符。

损失能量后轨道半径会不断变小
玻尔的巨大贡献是做出了两个非经典假设。第一是假设存在静止的电子轨道,这与经典物理学相悖。然后,他通过假设轨道电子的德布罗意波必须“匹配”或“同相”来指定这些轨道,因为电子进行了一次完整的旋转。如果没有这样的匹配,在每转一圈的过程中会发生一些振幅的抵消,波就会消失。
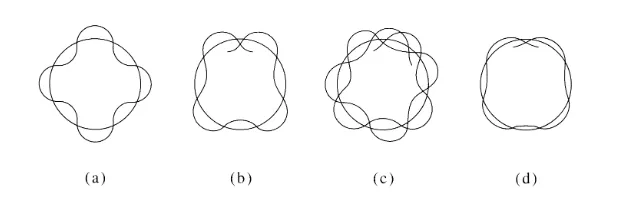
(a)图中的德布罗意波的波长整数倍适合于圆,可以持续传播;
(b)图中的德布罗意波的波长整数倍不适合于圆,持续传播后如(c)图后会抵消至(d)图完全消失。
为了使轨道周围的波型稳定,我们得出了一个条件,即轨道周围必须有整数个完整的波长。因为圆的周长是2nr,所以我们有量子条件
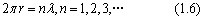
我们将等式1.2代入1.6中,得到
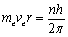
或
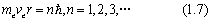
其中ħ=h/2π,称为约化普朗克常数,因为其适用范围很广,所以采用这种速记形式。
联立等式1.5和1.7,可以求出轨道半径
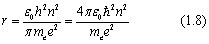
这就是量子化之后的原子轨道,称为波尔轨道。电子不能像宏观的圆周运动一样,穿行在任意半径的轨道上,而是只能在等式1.8所给出的轨道上。
我们将物理量带入上式中,
ε0=8.85419×10-12 C2·N-1·m-2,
ħ=1.055×10-34 J·s,
me=9.103×10-31 kg,
e=1.6022×10-19 C,
取n=1,计算氢原子中电子轨道的最小半径,
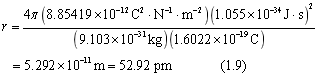
这个第一波尔原子轨道通常被标记为a0。
04
尾声
玻尔理论在旧有的理论上,做出了大胆的假设和创新,并在此基础上计算出了氢原子通常的半径,我们将在下一节来验证一下这个半径的正确性。
END
















