
最密堆积的晶胞(2)
六方最密堆积
在六方最密堆积中,由于可以通过存在六重轴或六重反轴旋转,使得原子周围环境完全相同,因此其晶胞被称为六方晶胞。
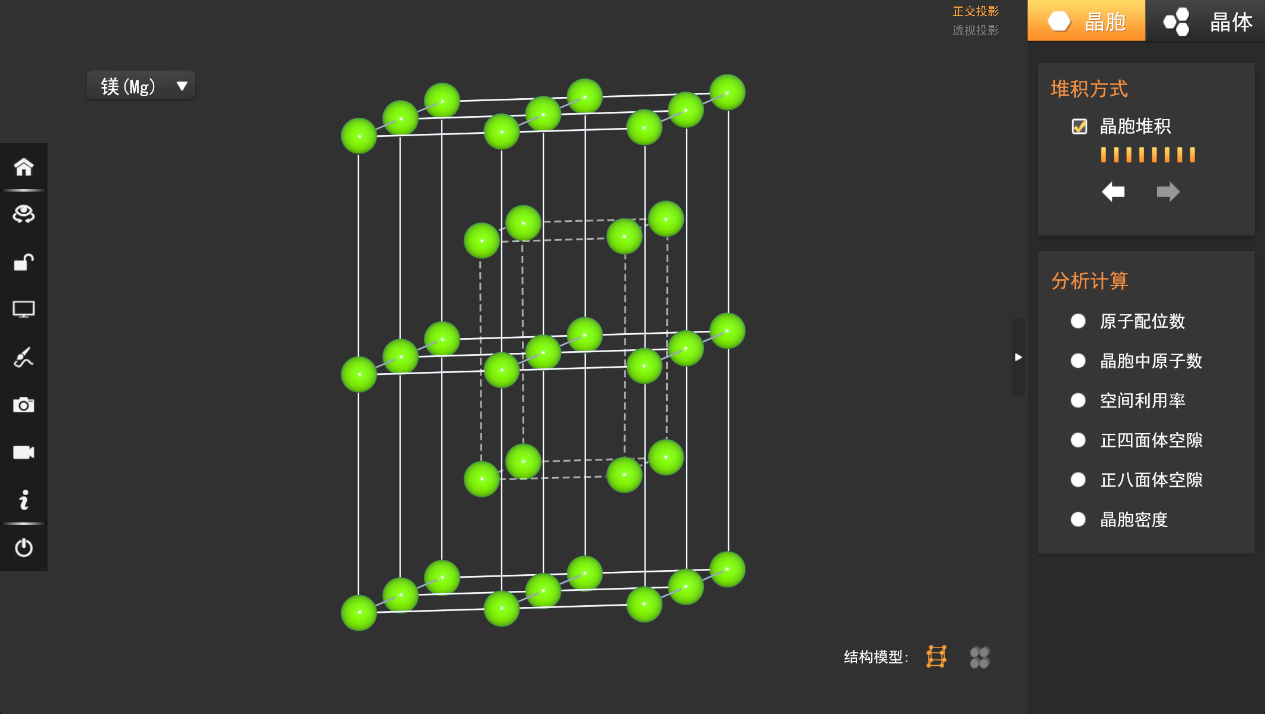
借助虚拟仿真平台进行观察,虚线框起来部分看起来也是一个晶胞,但实际上不能由实线部分的晶胞平移而来。
为了便于理解,我们将晶胞内部各个原子的位置以坐标来表示,即原子的坐标参数。在镁的六方晶胞中,Mg的坐标参数为:
顶点:(0,0,0)
内部:(2/3,1/3,1/2)
在晶胞中,我们可以发现总共有9个原子,但是坐标参数却只有2个,其原因在于顶点的原子由6个或12个晶胞共享,每个晶胞只有1/6或1/8个原子。
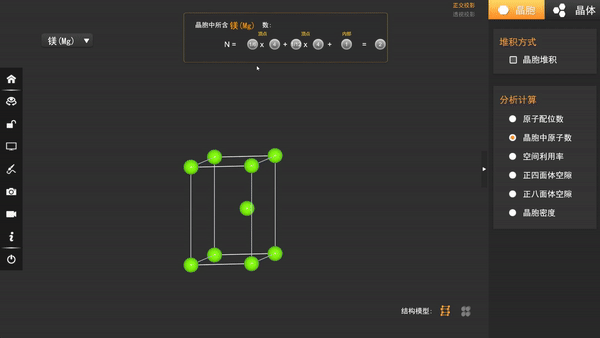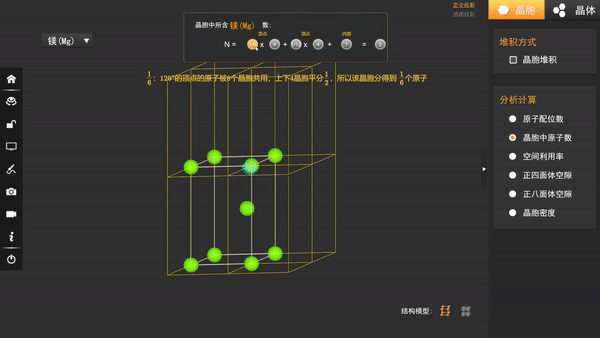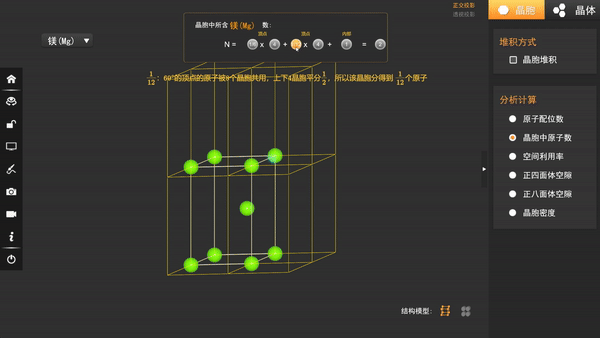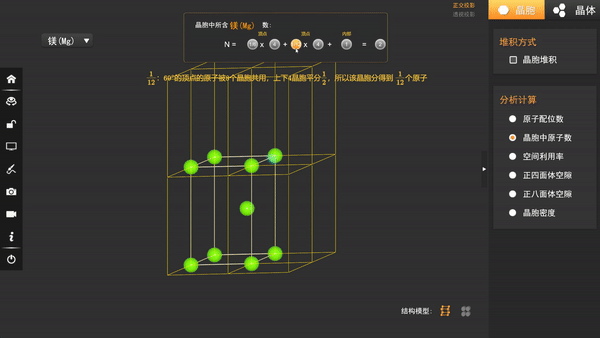
晶胞内部的原子由晶胞独享。
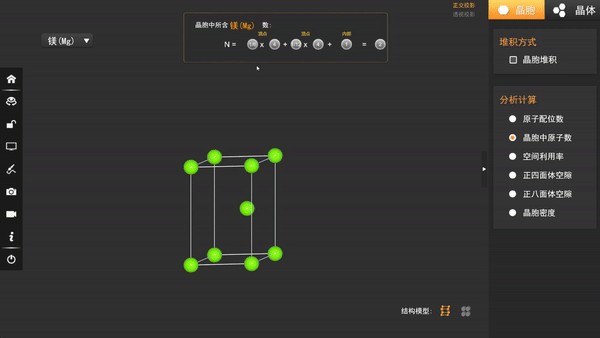
最终,由于每个晶胞有8个顶点和6个面,因此每个晶胞的原子数为:
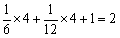
同样的,我们可以通过计算来确定六方晶胞的空间利用率。
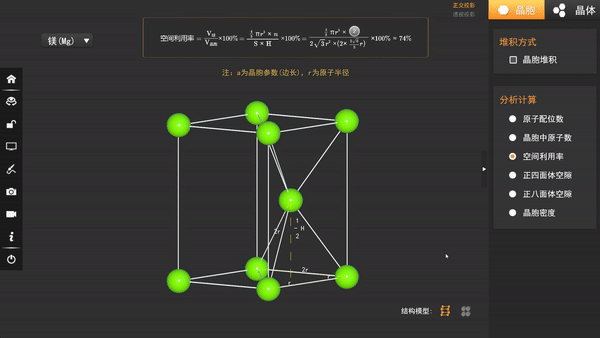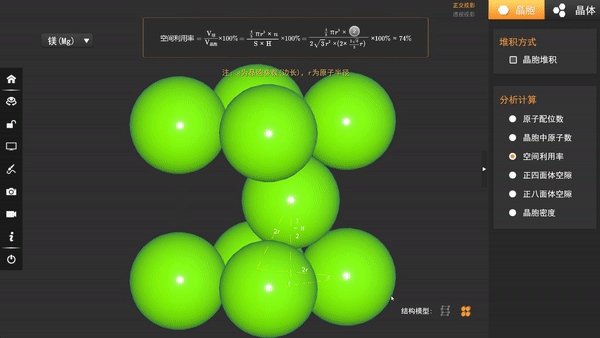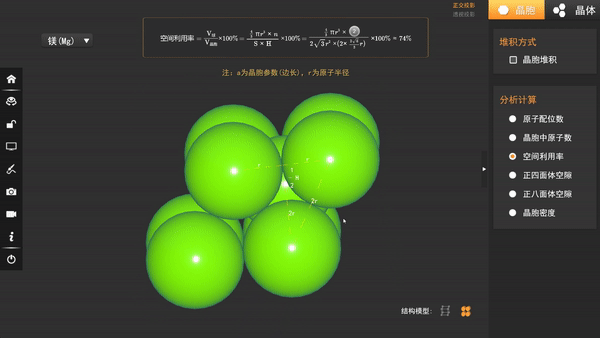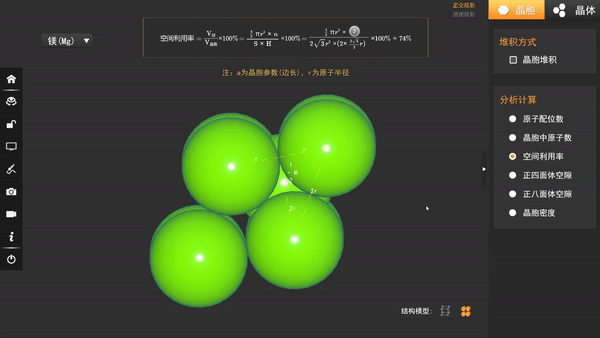
设球的半径为R,晶胞底面菱形边长为a,由于最密堆积,边长也为2R,所以a=2R,底面面积
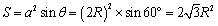
设晶胞高度为c,可以看出相当于两个正四面体的高,因此
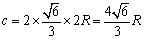
晶胞体积
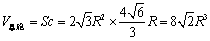
晶胞中两个球的体积
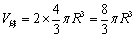
空间利用率
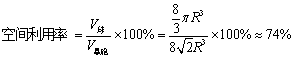
此时我们发现六方最密堆积的空间利用率与立方最密堆积相等,这并不奇怪——都是最密堆积,且对于每一层而言都只是被填了一半的空隙。
类似地,我们可以计算晶胞的密度。Mg的原子半径是160 pm,摩尔质量是24.31 g/mol,那么晶胞密度
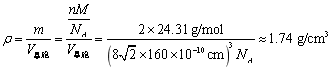
通过查询可以得知Zn在20℃时的密度为1.738 g/cm3,误差也很小了。

我们会发现,当从微观角度出发,会发现物质的很多性质是由结构影响的,原子的结构、原子堆砌的结构都会影响宏观的性质,这也体现了化学中“结构决定性质”的思想。
END
















