【矩道虚拟仿真实验室】虚数的真实（一）

到1500年左右，零已被人接受作为一个数，无理数也用的更随便了，但是仍然有数学家对于无理数的态度仅仅是作为记号，不能当作实际存在的数。甚至牛顿在他的《普遍的算术》中也持有这一观点。

负数则更为曲折，虽然通过阿拉伯人的著作传入欧洲，但是16世纪和17世纪的大多数数学家并不承认它们是数，或者不是方程的根。

欧洲人在还没有完全克服无理数和负数带来的困难时，就又无意地陷入虚数的问题中。他们在使用配方法解二次方程时碰到要把开平方推广到其他数的时候，得到了这些新的数。而卡尔达诺在解三次方程时，还要进一步地与虚数打交道。

吉罗拉莫·卡尔达诺（Girolamo Cardano, 1501~1576）

同样的，对于虚数的实际意义，当时的大部分数学家包括牛顿都持否定态度。事实上，他在《普遍的算术》中说过：“正是方程的根出现不可能的情况（虚数），才导致不可解的问题像是可解的样子。”也就是说，在物理和几何上没有实解的那些问题，应该会出现虚数根。

然而事实真的如此么？

就像负数的使用不可避免地与“相反”这一概念扯上关系，虚数也可以与某一种概念对应上。

我们把乘法看作是“变换”，具体的变换规则由后面的乘数来确定。例如，“×1”是保持不变，“×-1”是变成相反数，“×2”是放大为原来的两倍，“×0.5”是缩小到原来的一半。

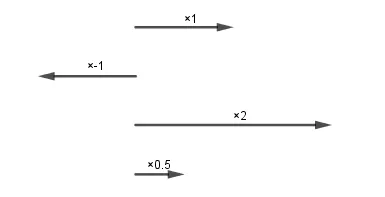
我们在此使用“变换”并不会改变乘法的计算法则，只是改变了看待问题的角度。

我们现在来考虑一个稍微复杂一点的问题——“×x^2”，这就相当于是“×x×x”，即对于原来的数进行两次相同的“x变换”。当x^2=1时，结果意味着我们经过两次相同的变换又得到了原来的数。显而易见地，这两次相同的变换要么都是“×1”，要么都是“×-1”。

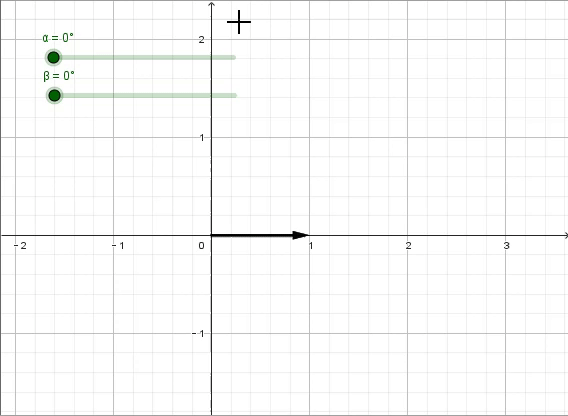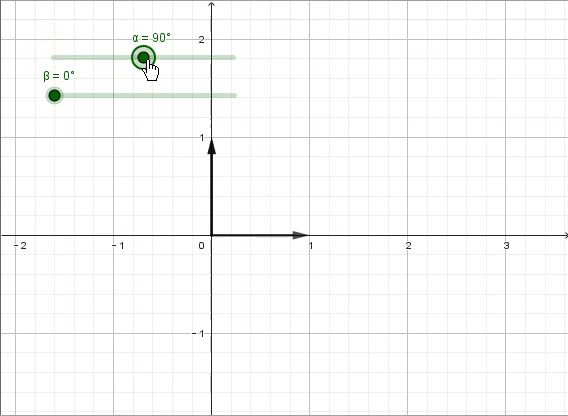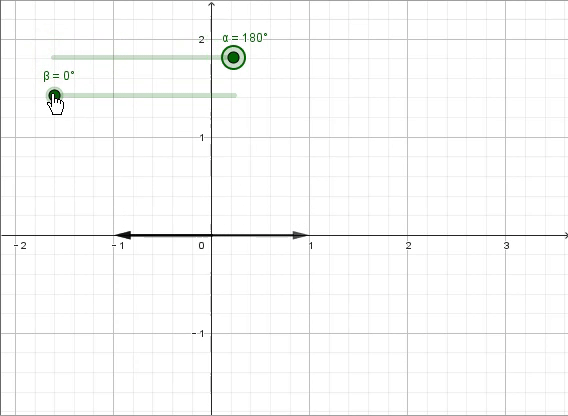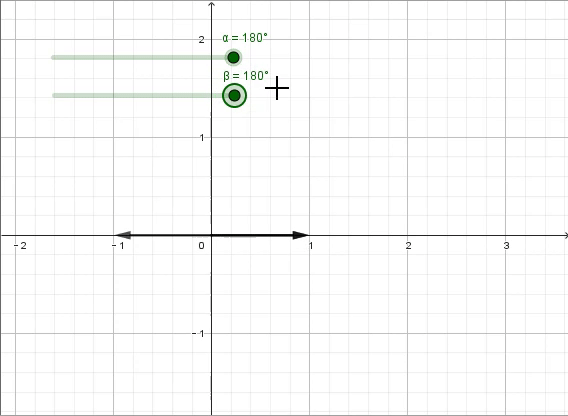
接下来，我们把问题再复杂一点，当x^2=-1时，意味着我们经过两次相同的变换得到了原来的相反数，那么此时的“x变换”会是什么呢？

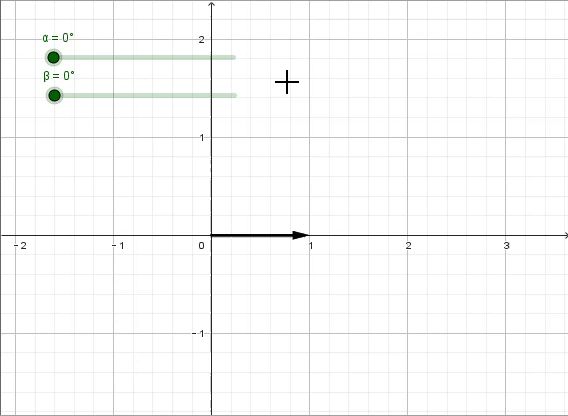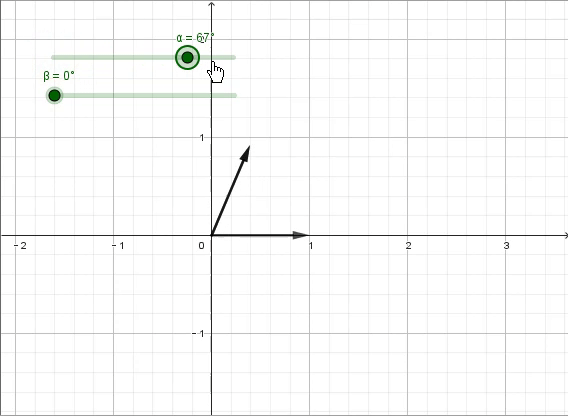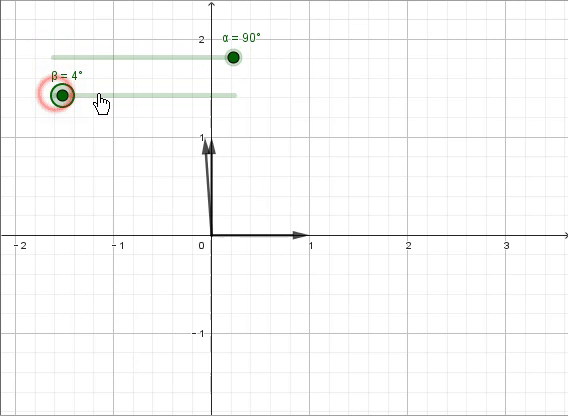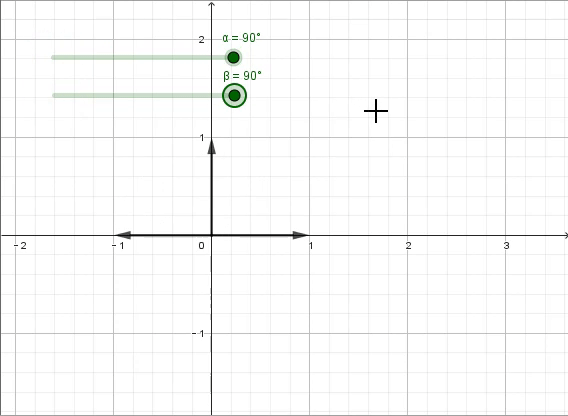
答案是“旋转”，更具体一点讲，是“逆时针旋转90°”。连续两次的“逆时针旋转90°”，就得到了原来的相反数。此时我们需要垂直于原数轴的第二根数轴，并用i来表示此时方程的解，特制“逆时针旋转90°”的变换。

那么，如果是想顺时针旋转90°呢？

那就只要×-i就行。

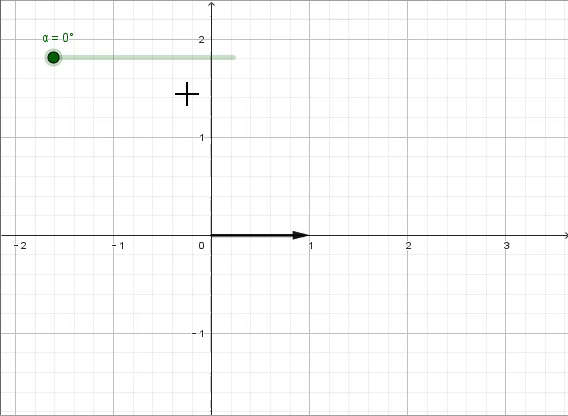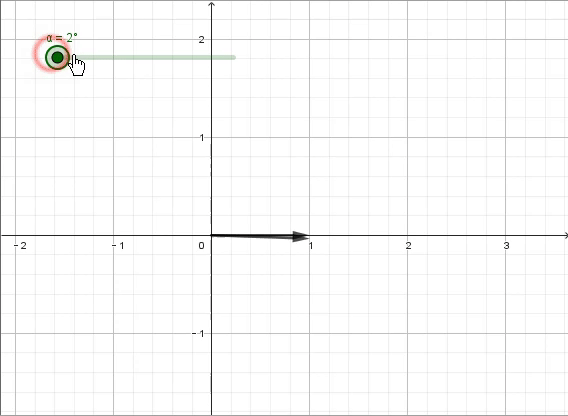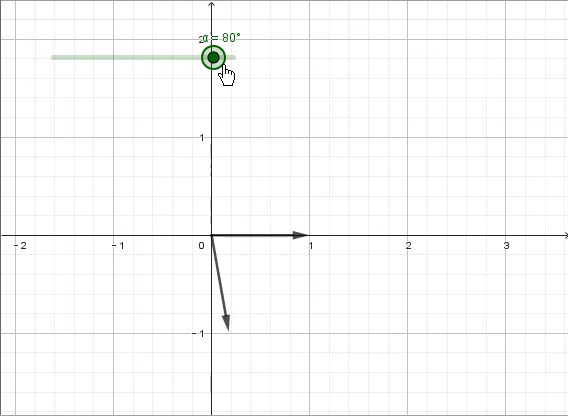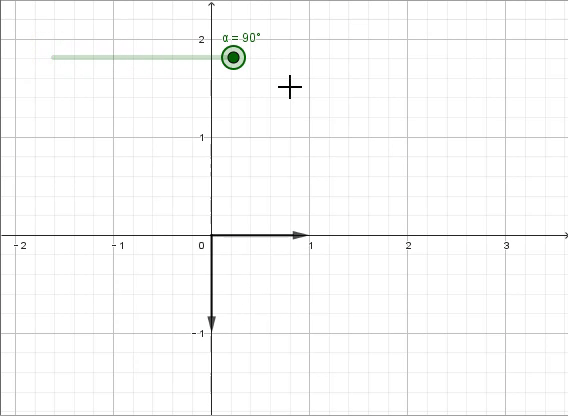
在这个过程中，我们也将一维的实数域拓展到了二维的复数域——实轴上有所有的实数（包括有理数和无理数），虚轴上则有所有的虚数，而其他的地方就是实数与虚数的复合，即复数。复数可以表示为a+bi的形式，a为实部，b为虚部，对应复平面内的点(a,b)——比如一个复数z实部是1，虚部是2，就可以表示为z=1+2i，对应复平面内的点(1,2)。

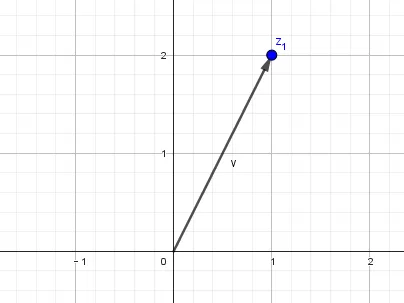
因为复平面内的点Z(a,b)与以原点为起点、以Z(a,b)为终点的向量OZ一一对应，所以复数z=a+bi也可以用向量OZ来表示。

实数相互之间是可以比大小的，但是复数并不存在大小的概念，因此我们将向量OZ的模叫做复数z=a+bi的模(module)（或绝对值），记作|z|或|a+bi|，由模的定义可知

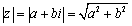
同时，以x轴的非负半轴为始边、向量OZ所在的射线为终边的角θ叫做复数z=a+bi的辐角（argument）。很明显，任一非零的复数z=a+bi的辐角有无数个值，这些值之间相差2π的整数倍。我们把其中适合于0≤θ≤2π的辐角的值叫做复数z=a+bi的辐角主值，记作arg z。

若将复数z=a+bi的模设为

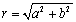
辐角设为θ，则复数z也可表示为

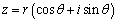
称为复数的三角形式。