矩道3D教学软件
From Zero to Infinity

在前两篇文章中,我们讲述了“一一对应”的关系,而集合论创始人康托尔就用这种方法巧妙证明了自然数、整数、奇数、偶数的个数是一样多的,他把这样多的个数称为可数无穷大,这些结论显然违背我们的生活常识,但上述集合中元素“一一对应”的关系却是严格的。
01
对于第一期我们提到的问题3:
一条直线上的点构成的集合,和一个圆上的点构成的集合的元素个数,哪个更多?
如果我们能找出来一种让直线上的点与圆上的点“一一对应”的关系,那就可以证明两者个数相同。举例如下:
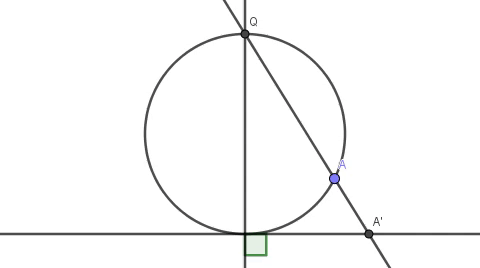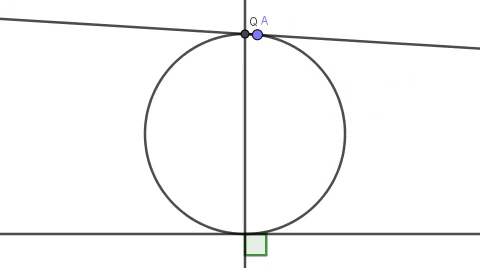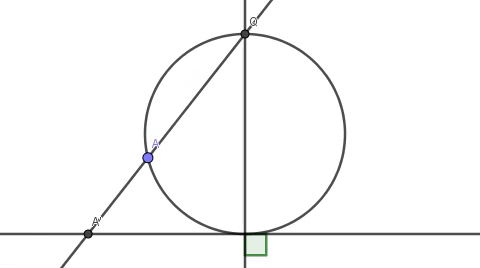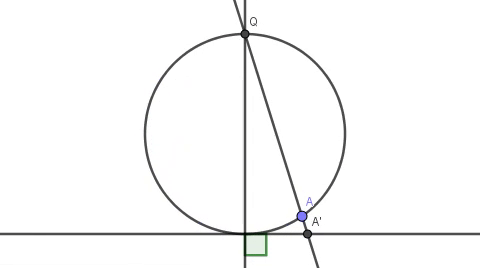
过Q点与圆上任意一点A作直线与已知直线相交于A’点,QA就建立了圆上的A点与直线上的A’点“一一对应”的关系。除了一个点——Q点本身。
当A点与Q点不重合的时候,圆的割线QA与已知直线不平行,所以必然存在一个交点A’。而当A点与Q点重合的时候,圆的割线QA将变成过Q的切线,此时与已知直线平行,无交点,是不是意味着圆比直线多一个点Q呢?

02
平行线是否相交?
关于平行线是否相交其实是个历史问题,关系到几何的发展史。
最开始,在欧洲古代,在中国的战国时期,希腊有个非常非常厉害的人,叫欧几里得,他和屈原是一个年代的人,屈原写了《离骚》,他写了一本书,叫《几何原本》,它几乎是所有几何问题的鼻祖。欧几里得在书里,规定了五条公理,其他的一切几何问题,都由这五条公理推导出来,我们中学学习的关于平面几何的内容,几乎都处于其中。

欧几里得(希腊文:Ευκλειδης )
约公元前330年—公元前275年
《几何原本》,可以说是人类历史上最伟大的著作之一了,他在书中提出的前四条公理都很简单,比如:过两点可以作一条直线;直线可以无限延长;过圆心一点用已知半径可以做一圆;直角都相等。唯有第五条公理,比较复杂,不像前面那四条一目了然,且全书最后才用到:
如果一条线段与两条直线相交,在某一侧的内角和小于两直角和,那么这两条直线在不断延伸后,会在内角和小于两直角和的一侧相交。
或等价于:
给定一条直线,通过此直线外的任何一点,有且只有一条直线与之平行。

03
关于第五公理:
文艺复兴后,科学家对这个第五公理很困惑,尝试证明它,都失败了。后来俄国数学家罗巴切夫斯基用反证法来尝试(在一个平面上,过已知直线外一点至少有两条直线与该直线不相交),看看能不能推导出有意义的结果,结果奇迹出现了,如果两个平行线也能相交的话,会出现另外一套几何理论,后来称之为罗巴切夫斯基几何。

尼古拉斯·伊万诺维奇·罗巴切夫斯基
(1792.12.1.-1856.2.24)

04
非欧几里得几何
继罗巴切夫斯基后,德国数学家黎曼在1854年又提出了既不是欧氏几何也不是罗氏几何的新的非欧几何。
这种几何采用如下公理替代欧几里得平行公理:同一平面上的任何两直线一定相交。人们把黎曼所发现的几何与罗氏几何统称为非欧几何。虽然这个非欧几何在之后的几个世纪毫无用处,谁也没想到20世纪的爱因斯坦会依靠它研究出了广义相对论。
我们平时说的几何,都是欧氏几何,就是屈原同辈的欧几里得研究的几何,都是在他的五条公理下面的几何,即两个平行线不能相交。但在非欧几何(非欧几里得几何)下,显然两条直线相交于无穷远处,那此时点Q就会与这个相交于无穷远的点对应。

05
另一种可能
如果不考虑平行线相交这种“反常识”的知识点(虽然我们最近已经接受了很多“反常识”了),我们不妨接受圆比直线多一个点这个结论,因为这个结论并不能说明两者的元素个数不同。
不要忘了,在希尔伯特旅馆中,即使来了一个20人的大巴车,我们也可以让所有的旅客都住进来。相比于无限而言,“多一个”、“少一个”甚至“多几个”、“少几个”都只是可以忽略不计的零头而已。所以如果不严谨的来看,我们已经找到了让圆比直线只多了一个点这种有限数量的方法,那已经可以宣布——一条直线上的点构成的集合和一个圆上的点构成的集合的元素个数是一样多的了。
END


















