简介
这一课讲的主要内容是借助矩道物理融合创新实验室软件解析高中阶段的直流电路。相比于初中阶段,高中阶段主要考察考虑了电源内阻的闭合电路欧姆定律,其次电路要稍复杂一些,滑动变阻器除限流接法外,还有分压接法。除此之外,题型与整体上的解题思路并没有多大区别。
解题思路
首先要正确判断电路类型,其次要分清电表所测对象,如果电路复杂,画出简化的等效电路图,在此基础上判断出各物理量的变化。
基本思路是“局部→整体→局部”,即从阻值变化的元器件入手,由串并联规律判知电路总电阻的变化情况,再由欧姆定律判断电路总电流和路端电压的变化,最后由部分电路欧姆定律及串联分压、并联分流等规律判知各部分的变化情况。

如果电路中只有唯一的变量,则可采用“串反并同”的原则进行判断。
“串反”是指某一电阻增大时,与它串联或间接串联的电阻,其电流、两端电压及功率都将减小;某一电阻增大时,与它串联或间接串联的电阻,其电流、两端电压及功率都将增大。
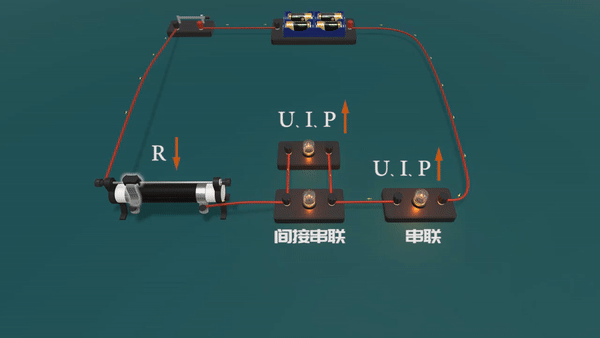
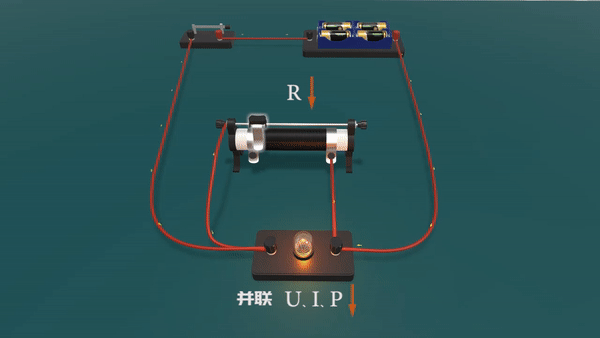
“并同”是指某一电阻增大时,与它并联或间接并联的电阻,其电流、两端电压及功率都将增大;某一电阻增大时,与它并联或间接并联的电阻,其电流、两端电压及功率都将减小。
例1
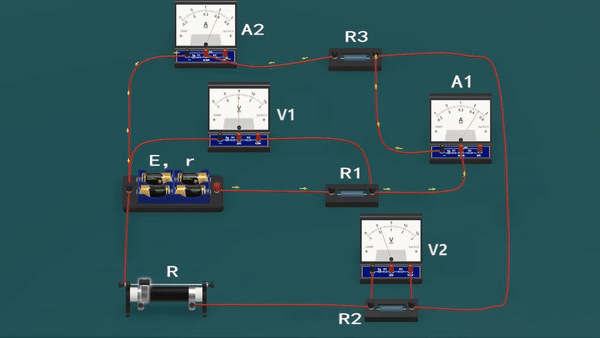
如图所示的电路中,图中四个电表均为理想电表,当滑动变阻器滑片P向右端移动时,下面说法正确的是( )
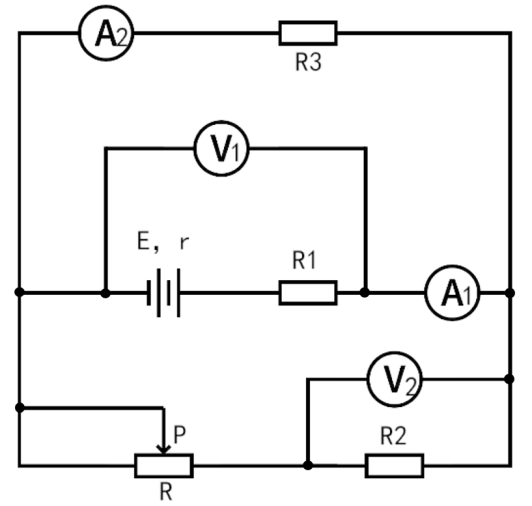
A.电压表V1的读数减小,电流表A1的读数增大
B.电压表V1的读数增大,电流表A1的读数减小
C.电压表V2的读数减小,电流表A2的读数增大
D.电压表V2的读数增大,电流表A2的读数减小
【演示】
当滑片P向右端移动时,电压表V1的读数减小,电流表A1的读数增大,电压表V2的读数增大,电流表A2的读数减小,因此答案选AD。
【解析】
本题电路较为复杂。滑动变阻器R与电阻R2串联后,与R3并联,然后再与R1串联。电压表V1测量并联部分的两端电压,V2测量R2两端电压,电流表A1测量干路总电流,A2测量R3电流。
实际上,R1在题目中不起作用,可忽略不计,或与内阻r合看作电源内阻,等效电路图如下:
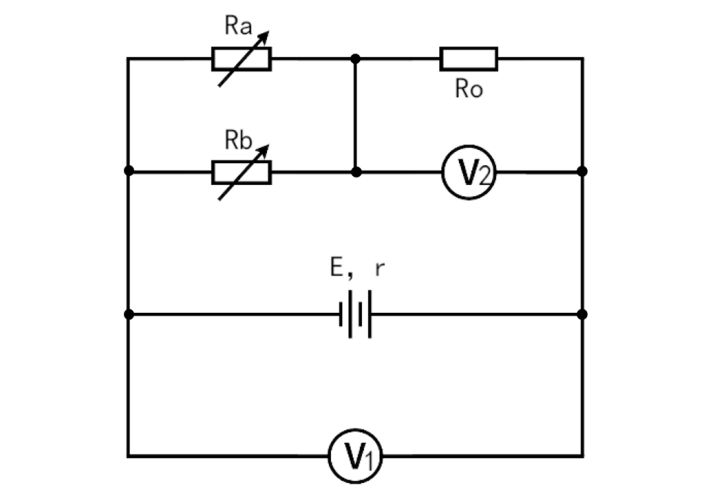
等效电路图
则,滑片P在向右滑动过程中,滑动变阻器R减小,则R总减小,I总即A1示数增大,U端即V1示数减小;而U端减小,则通过R3的电流、即A2示数减小;A1增大,A2减小,则通过R2的电流增大,从而R2两端的电压、即V2增大。
根据“串反并同”的方法也很好判断,R2与R串联,R3与R并联,R1、r与R串联。则R减小时,R2及R1、r的I、U、P等物理量皆增大,所以V2、A1增大,R3的I、U、P等物理量皆减小,所以V1、A2减小。
例2
如图所示电路中,电源电动势和内阻分布为E,r,R0=r,滑动变阻器的滑片P由a向b缓慢移动,则在此过程中( )
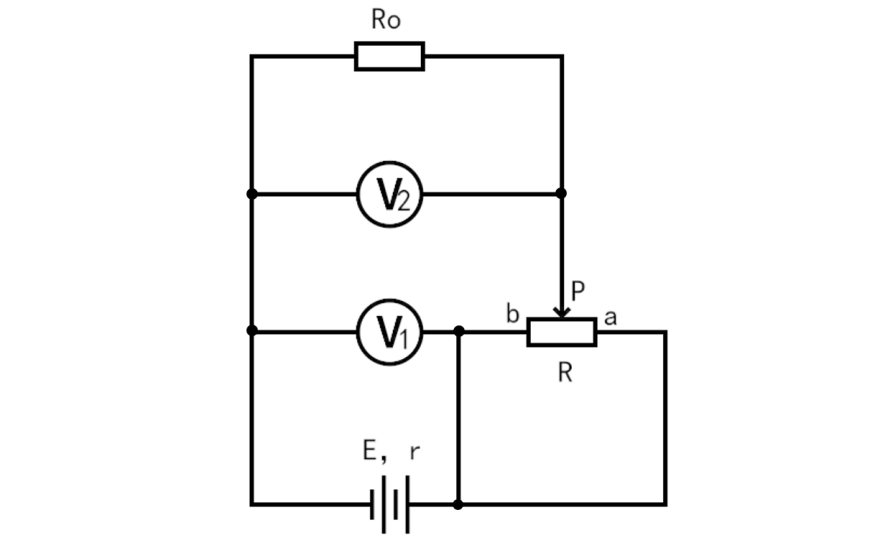
A.电压表V1的示数一直增大
B.电压表V2的示数先减小后增大
C.电压表V2的示数一直增大
D.电源的总功率先减小后增大
【演示】
滑片P由a向b缓慢移动过程中,电压表V1的示数先增大后减小,电压表V2的示数先减小后增大,电源的总功率先减小后增大,因此答案选BD。
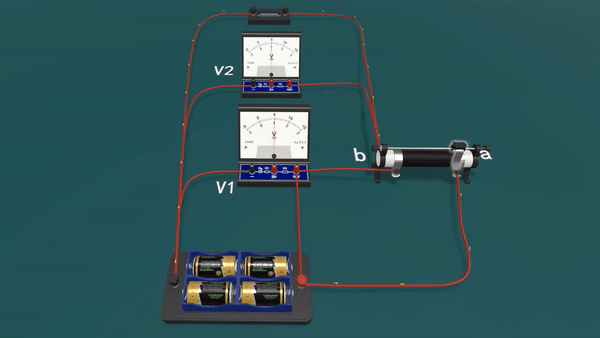
【解析】
本题的难点在于分析滑动变阻器的接法及其阻值的变化。可由节点法判断出滑动变阻器左右两端同时接入了电源正极,属于并联,然后共同由滑片端与R0串联。而电压表V1两端与电源正负极相连,测量的是路端电压。电压表V2测量的是R0两端的电压。因此等效电路图如下所示:

等效电路图
当滑片在a端时,滑动变阻器右端电阻为0,相当于滑动变阻器短路,并联部分的电阻为0;当滑片在b端时,滑动变阻器同样被短路,电阻为0;因此可判断出R并先增大后减小。
此外,还可用数学的方法得到。
当滑片从a到b滑动时,设a端接入阻值为Ra,则并联部分的电阻R并为:
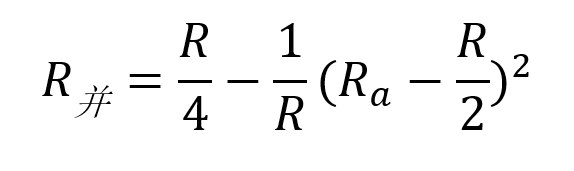
可以看到,随着Ra的增大,R并也在增大,当滑片滑到中点Ra为R的一半时,并联部分的电阻达到最大。
因此,滑片从a到b滑动过程中,R并先从0增大到最大值,再减小到0。从而R总先增大后减小,I总先减小后增大,U端即V1示数先增大后减小;由I总的变化可得知R0两端电压即V2的示数先减小后增大,电源总功率P总=EI总先减小后增大。
例3
如图所示的电路中,闭合电键S,当滑片P向右移动时,灯泡L1、L2的亮度变化如何?
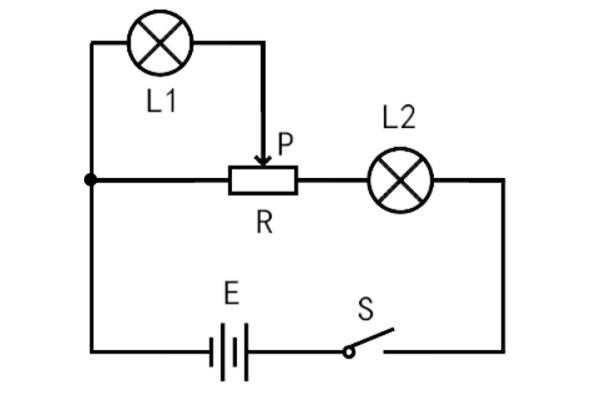
【演示】
当滑片P向右移动时,灯泡L1、L2均变亮。

【解析】
滑动变阻器的连接情况如下图所示:
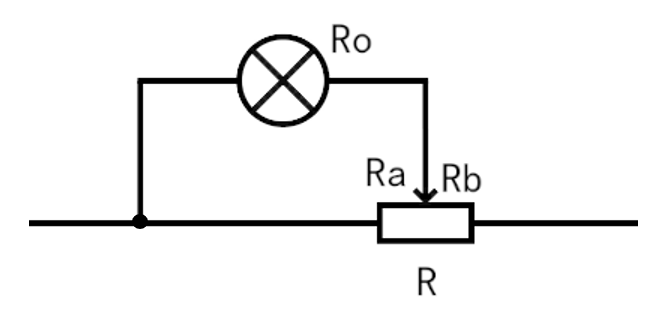
在这种情况下,滑动变阻器可分成两段,其中一段与用电器并联,然后再与另一段串联,总阻值R总有
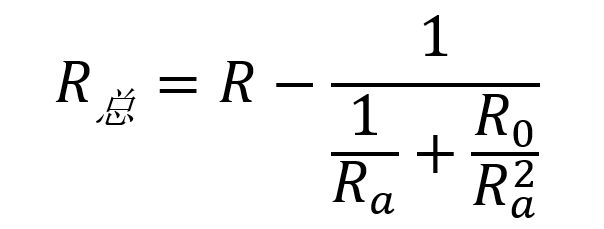
可以看出,当Ra增大、Rb减小时,R总在增大;当Ra减小、Rb增大时,R总在减小。
题目中,可将L2与串联段电阻合看作一个整体。因此,当滑片P向右移动时,并联段电阻增大,分压增大,L1变亮;而总电阻变小,则总电流增大,则L2也变亮。
总结
矩道物理虚拟仿真实验平台,是物理老师的自由创作工具,辅助老师进行物理模型建构与场景式教学的探索。通过提供高自由度、并遵循经典物理规律运行的探究环境,能够实现现实中无法实现的如天体运动、电场线与等势面、匀强及周期性电磁场等理想物理模型建构,还能将抽象的题目转化为真实的过程,将题目情境化、可视化,厘清复杂的物理过程。
















