原子空间利用率是指金属原子在整个晶体空间中所占有的体积百分比。可以用数学表达式表述为:
空间利用率 = 球体积 / 晶胞体积 × 100%
让我们使用矩道化学VR实验室软件来详细介绍一下金属晶体原子空间利用率的计算方法。
简单立方晶胞

原子均位于立方体顶点,其微粒数 = 8×(1/8)=1
球体积 = 4πr³ / 3 × 1

晶胞体积 = (2r)³
原子空间利用率 = 球体积 / 晶胞体积× 100%
= (4πr³ / 3 × 1) / (2r)³ × 100% ≈ 52.36%
体心立方晶胞
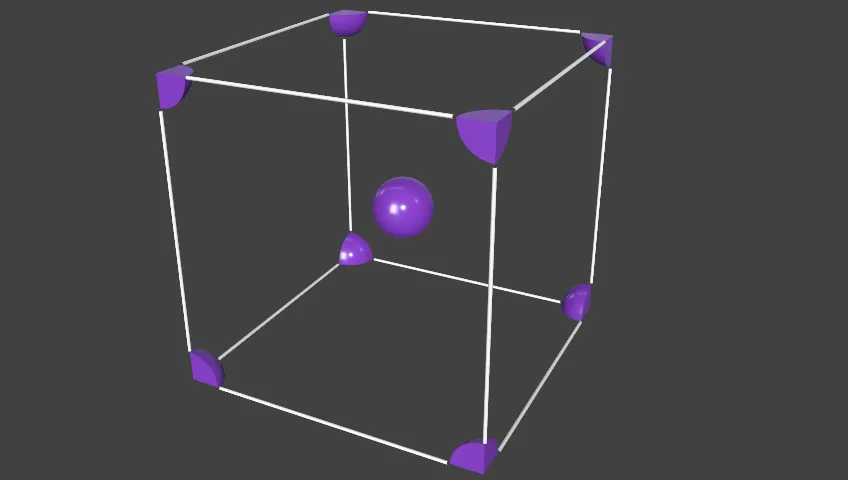
晶胞顶点处有8个原子,体心处有1个原子
即一个晶胞所包含的原子数 = 8 × (1/8) + 1 = 2
球体积 = 4πr³ / 3 × 2

设晶胞的边长为a,金属原子的半径为r,则晶胞对角线长为c = 4r,4r = √3 a,a = 4r / √3
原子空间利用率 = 球体积 / 晶胞体积 × 100%
= (4πr³ / 3 × 2) / a³ × 100% ≈ 68.02%
面心立方晶胞
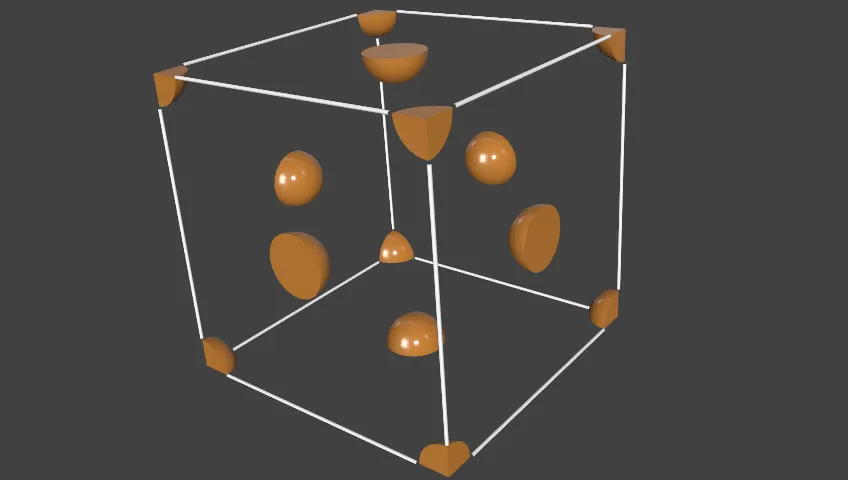
面心立方晶胞中,金属原子占据了8个顶点和6个面心,其原子个数= 8 × (1/8) + 6 × (1/2) = 4
球体积 = 4πr³ / 3 × 4
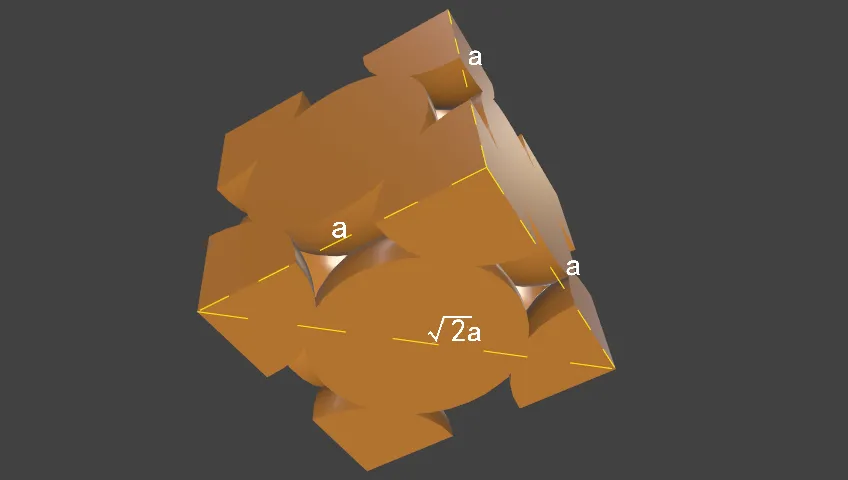
根据立体几何可知4r = √2 a,即a = 2√2 r
原子空间利用率 = 球体积 / 晶胞体积 × 100%
= (4πr³ / 3 × 4) / (2√2r)³ × 100% ≈ 74.05%
六方最密堆积晶胞
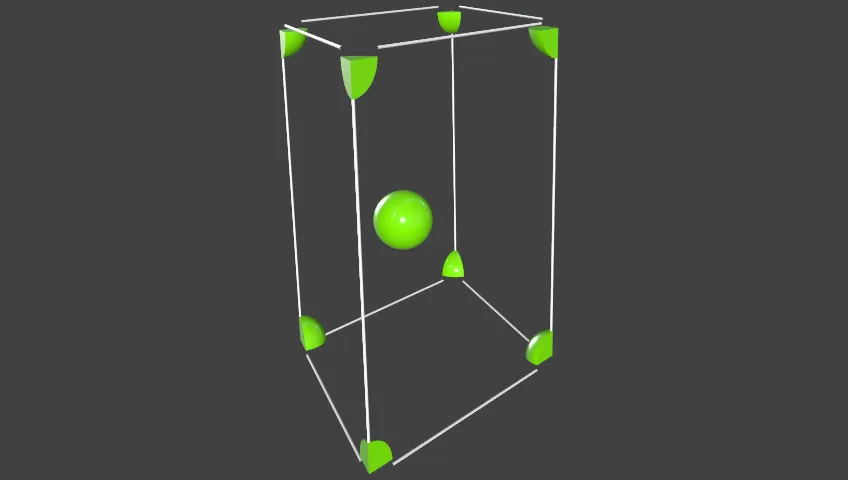
六方最密堆积晶胞中有2个金属原子,即球体积= 4πr³ / 3 × 2

晶胞底部是平行四边形,各边长a = 2r,因此平行四边形的面积S = a × asin60° = √3 a² / 2

晶胞的高h = 2 × 边长为a的正四面体的高 = 2 × √6 a / 3
因此,晶胞体积V = S·h
= (√3 a² / 2)·(2 × √6 a / 3) = √2 a³ = 8√2 r³
原子空间利用率 = 球体积 / 晶胞体积 × 100%
= (4πr³ / 3 × 2) / (8√2 r³) × 100% ≈ 74.05%
















