【矩道化学虚拟实验室】原子结构(二)

约翰·雅各布·巴耳末，原本是一名默默无闻的数学教师，直到60岁才取得重要的成就——巴耳末公式，对近代原子物理学的发展产生了重大影响。

一段时间以来，科学家们已经知道，当受到高温或放电时，每个原子都会发射出具有特征频率的电磁辐射。在焰色反应中，某些金属或它们的挥发性化合物在无色火焰中灼烧时使火焰呈现特征的颜色的现象就是这种辐射的宏观表现之一。

光的双缝干涉实验验证了光的波动性

换句话说，每个原子都有一个特征发射光谱。由于原子的发射光谱仅由某些离散的频率组成，它们被称为线谱。

氢是最轻、最简单的原子，具有最简单的光谱。下图中反映了氢的部分光谱。

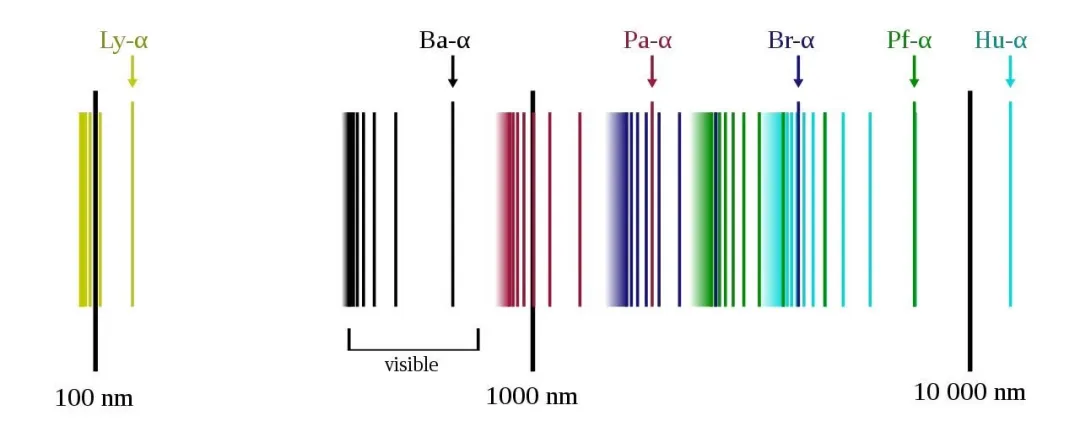
氢光谱的序列，坐标采用对数标尺

其中在可见光范围内，波长依次为656.5 nm、486.3 nm、434.2 nm、364.7 nm……

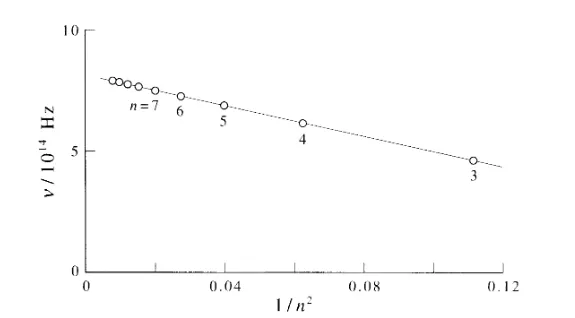
由于原子光谱是所涉及原子的特征，因此有理由怀疑光谱取决于原子中的电子分布。多年来，科学家们一直试图在氢原子光谱中找到谱线的波长或频率规律。

最后，在1885年，瑞士科学家约翰·巴耳末（Johann Balmer）证明了谱线的频率与1/n²（n=3,4,5…）的关系是线性的。

利用线性关系，巴耳末为这些谱线的波长确定了一个公共因子，写出了如下公式：

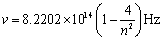
其中n=3,4,5…

为了方便后续研究，我们通常将该公式改写为

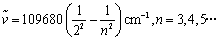
该等式称为巴耳末公式，其中

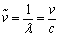
其中波长的倒数我们称之为波数，标准单位是m^-1，但是cm^-1的使用更广泛。

我们尝试带入一下n=4的情况，

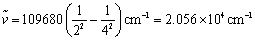
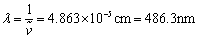
与前文中氢光谱可见光范围内第二条谱线波长相符合。

后来，瑞典科学家里德堡将巴耳末公式推广为如下形式，

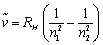
R_H为里德堡常数，现代值为109677.581 cm^-1，是已知最精确的物理常数之一。n₁和n₂均为正整数且n₂＞n₁，当n₁=2时，该公式即为巴耳末公式。而如果n₁=1、3、4……，就对应氢原子光谱中的其他谱线系列。

回过头来看，描述氢光谱的公式在某种意义上由两个整数控制，这真是令人惊讶。为什么氢原子要关心我们的整数？

原子在乎整数？

在19世纪90年代，里德堡发现了其中许多原子的近似经验定律。其他原子的经验定律通常更复杂，但真正有趣的是，这些差异都与整数有着关系。在当时，这只是一个等待理论解释的经验法则。