【矩道化学虚拟实验室】简单立方堆积的晶胞参数
更新时间:2023-03-06 来源:矩道科技 浏览:0

用虚拟仿真技术学习非密堆积的晶胞参数
简单立方堆积
简单立方堆积的晶胞由于八个原子都在顶角,原子坐标均为(0,0,0),所以只能按照坐标轴方向平移整数个单位来重叠。
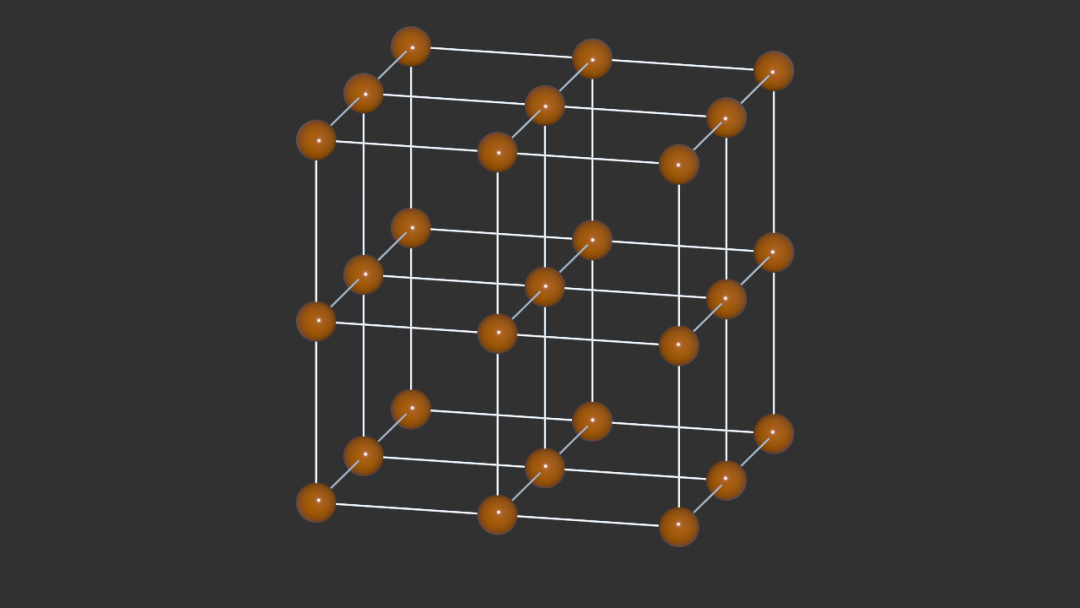
每个晶胞的原子数为
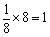
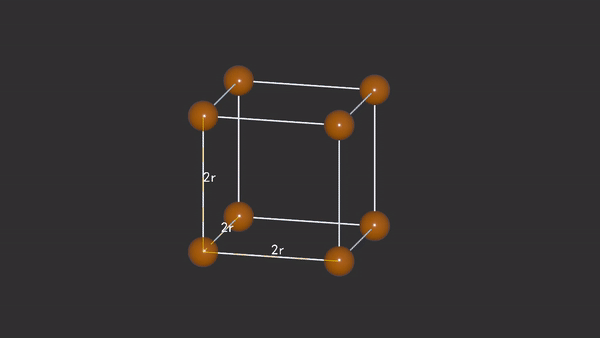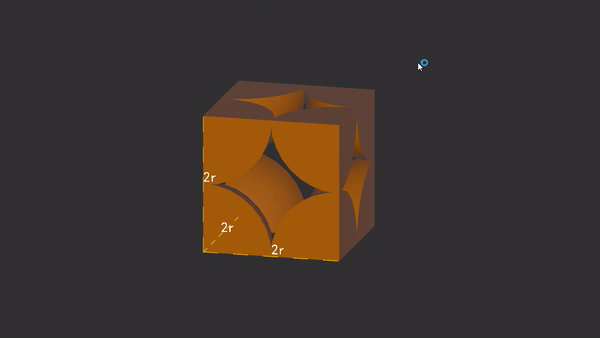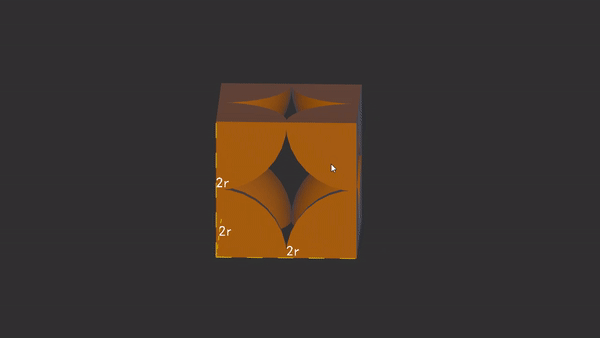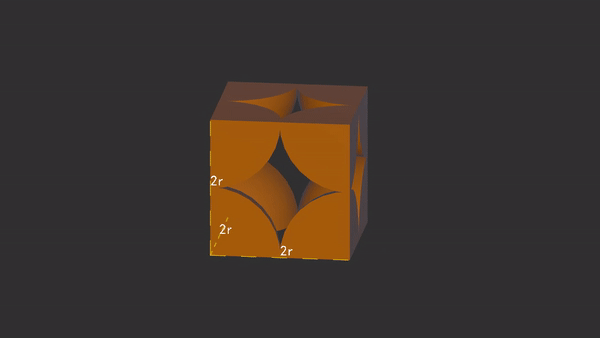
简单立方晶胞的密度计算相对来说要简单很多,设球的半径为R,晶胞边长为a,则
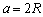
晶胞体积
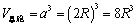
晶胞中球的体积

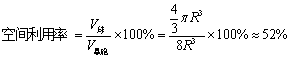
可以看出来在体心立方晶胞种,虽然看起来原子都是紧密相连,但是空间利用率很低,这是因为在原子堆积的时候,完全没有利用空隙,都只是简单的堆砌。

“巨大无比”的空隙
金属通常并不会采取这种堆积方式,结构很不稳定,常态下只有Po是唯一实例。当然也有猜想认为当时有其他比较小的原子填充在Po的晶胞中心,才导致出现这种情况。
Po的原子半径是168 pm,摩尔质量是209 g/mol,
那么晶胞密度
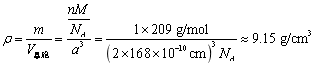
Po在室温下的密度为9.196 g/cm3,相对误差大约是5‰。
尾声
金属单质的堆积以两种最密堆积为主,因为最邻近的金属键对结构的稳定性起主要作用,较长的键贡献很少。非最密堆积的金属单质以体心立方密堆积为主,其他结构比较少见。这些结构的存在,表明影响金属单质结构的因素不是唯一的,参与成键的价电子数及其他轨道也有一定影响。同时,把金属原子视为等径圆球也不应绝对化。
一种金属单质采取哪种结构,既有内在原因,也受外界条件影响。研究表明,原子价层s,p电子数会影响晶体结构,d电子主要影响键的强度。
温度、压力等外部条件也会使金属单质结构改变,出现多种同素异构体。例如,Fe的晶体结构随升温会逐渐从体心立方(α相)→面心立方(γ相)→体心立方(δ相)。
END
















