矩道虚拟实验室——虚数的真实(二)
如果把复数z1、z2分别写成三角形式:
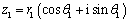
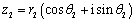
那么,依据乘法法则,就有
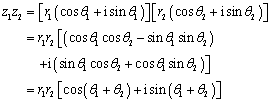
此时我们会发现,两个复数相乘,其积的模等于这两个复数的模的积,其积的辐角等于这两个复数的辐角的和。
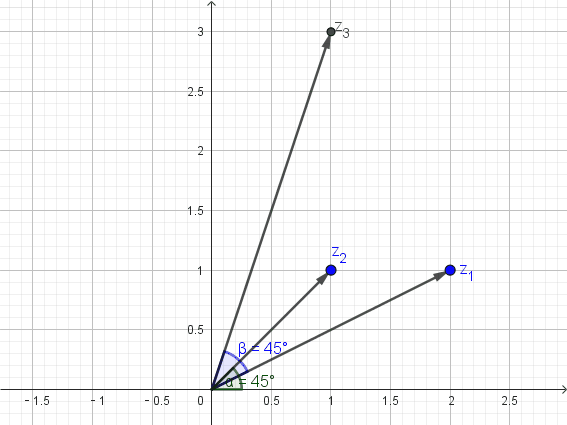
part01. 角度的旋转
假设我在一艘船上,每向北4个单位,就向东3个单位。我想把航向逆时针旋转45度,此时船的航向朝哪儿?

显而易见的,我们可以将当前的航向看作是3+4i,此时辐角为
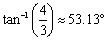
如果想逆时针旋转旋转45°,只需要将其与1+i相乘即可,因为1+i的辐角恰为45°。
计算过程可以看作:
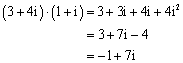
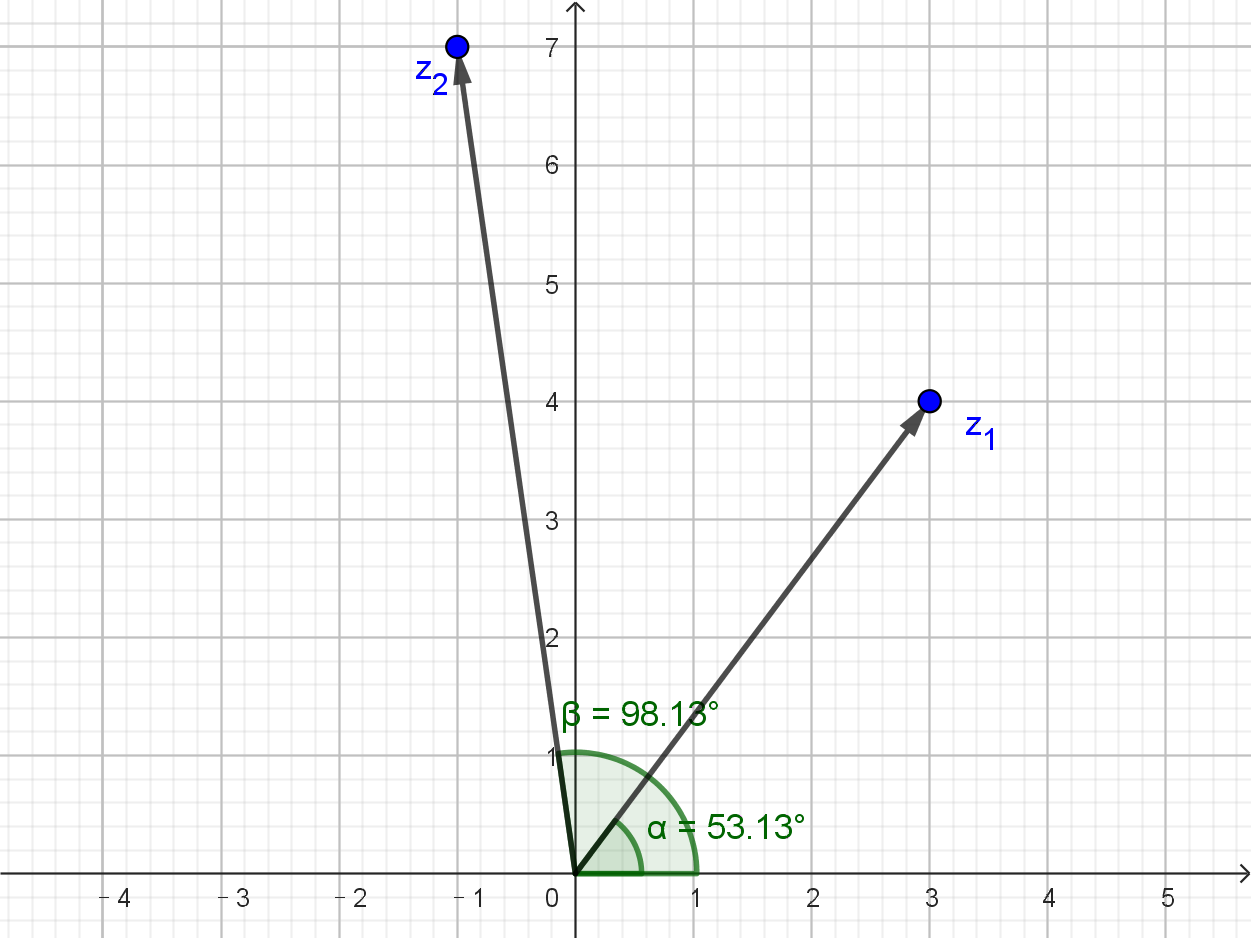
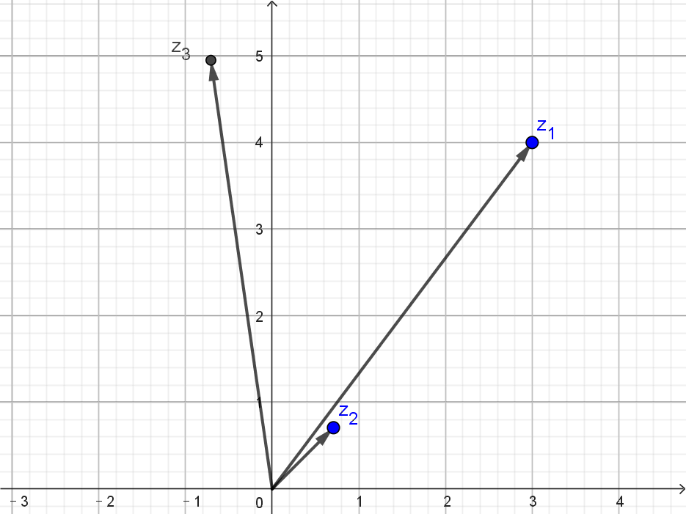
从图上我们可以看出来,此时航向是每向西前进一个单位,就向北前进7个单位。辐角是
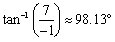
恰好等于原来的辐角加上45°。
part02. 模不变的旋转
当然,进一步地,如果我们将上述问题稍微更改一下,船的速度是每秒向北4个单位,向东3个单位,我想把航向逆时针旋转45度,速度不变,此时船速度的大小是多少?
我们仍然可以将原来的速度看作是3+4i,此时模为5。由于还是要逆时针旋转45°,所以还是乘以一个辐角为45°的复数。但很显然1+i已经不行了,因为上述结果-1+7i的模为5√2。
根据前述公式,我们需要找一个模为1辐角为45°的复数,则只需将1+i除以其模长即可
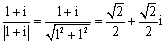
让其与3+4i相乘
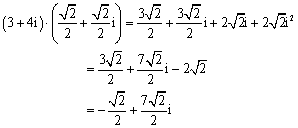
新的速度的模与辐角分别为:
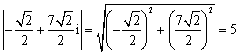
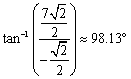
可以看到,此时速度大小与旋转前保持一致,方向逆时针旋转了45°。
上述计算的优势在于,我们并没有在调整航向时真的使用正弦余弦或是反正弦反余弦函数,只是用了乘法的基础运算(当然,还有一点小小的虚数i2=-1运算),但是却起到了旋转的作用。
而且,结果会很有用,我们有一个具体的航向(-1,7)而不是角度98.13°。这个角度并不精确,或者换个说法,你打算怎么在航海图上精确绘制并遵循这个角度呢?量角器么?
事实上,在缺少计算器的年代,你甚至只能通过查表的方式来得到一个不够精确角度(假设表上恰好有的话)。而在大海上,不够精确的角度大概会直接引导你到美洲新大陆吧。

而如果我们要顺时针旋转怎么办?是找一个辐角为-45°的复数么?还是找一个315°的复数?没必要这么复杂,我们只需要用原来的复数除以一个辐角为45°的复数即可,其原理各位同学可以课后自行证明。
因此我们可以看到,复数本身有大小、方向,在运算中也具有其意义——旋转,尽管看上去很奇怪,但它确实有着真实的含义。
END
















