原子中电子的总能量等于其动能和势能之和。电子和质子相隔距离r的势能由库仑定律给出
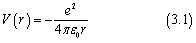
这里的负号表示质子和电子相互吸引时它们的能量小于它们无限分离时的能量V(∞)=0。
氢原子中电子的总能量为
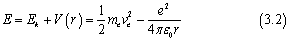
在第一篇文章中,我们有提到将氢原子中的电子运动看作圆周运动时有
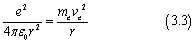
我们将meve2消掉,
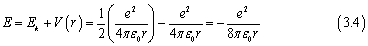
r的值同样在第一篇文章中由计算得出
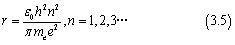
我们将其带入后,可以发现在氢原子中电子的能量为
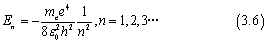
显而易见的,当n=1的时候,电子的能量最低,这种能量被称为基态能量。在常温下,氢原子以及大多数其他原子和分子几乎完全处于基态。较高能量的状态称为激发态,通常相对于基态是不稳定的。
玻尔假设氢原子的观测光谱是由于从一个允许的能量状态到另一个允许能量状态的转变,并且使用方程,他预测允许的能量差由下式给出
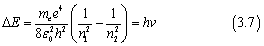
当电子从一个能级跌落到另一个能级时,能量将最终E=hv的光子形式释放,即会向外释放不同波长的电磁波。当激发到更高能级的电子跌落到n=2状态时,就会出现巴耳末谱系的电磁波。
我们可以将理论公式改写成经验里德堡公式的形式,
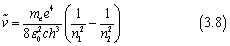
我们将里德堡公式与上式对比,可以得到
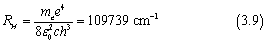
与里德堡常数的实验值109677.6 cm-1相比,误差在0.05%以内。而与里德堡公式不同的是,在玻尔模型的基础上,里德堡常数与量子数n都有了明确的含义。
电子在每一层有对应的能量,当电子从能量较低的内层转移到能量较高的外层时,需要吸收的能量将等于两层能量之差的绝对值,而不能是一个连续值。反之亦然,所以原子光谱不是连续谱线,而是一根根分散的谱线。
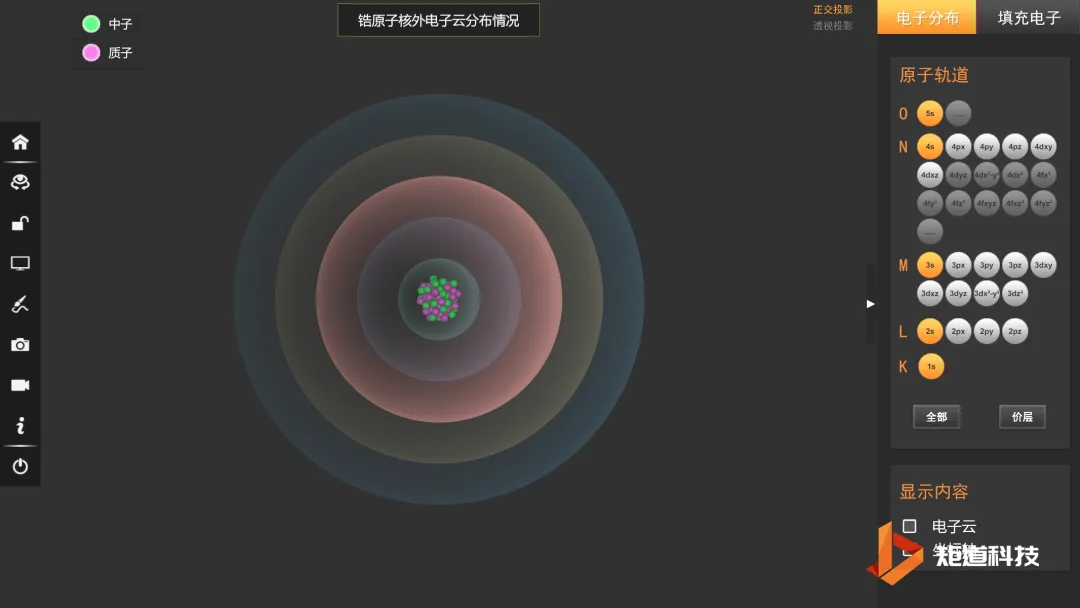
锆原子的核外电子层
尽管玻尔理论取得了许多成功,而且非常简单,但该理论甚至不能成功地推广到氦等双电子系统。此外,即使对于氢这样的简单系统,它也无法解释当磁场施加到系统时产生的光谱,也无法预测谱线的强度。
END

















